Fracciones En La Recta Numerica Para Niños De Primaria – Fracciones En La Recta Numérica Para Niños De Primaria, una aventura matemática que desentraña el fascinante mundo de las fracciones. A través de una narración envolvente, esta guía promete convertir conceptos complejos en lecciones comprensibles y agradables, empoderando a los jóvenes estudiantes a navegar por el reino de las fracciones con confianza y habilidad.
Desde entender la diferencia entre fracciones propias e impropias hasta comparar, ordenar, sumar, restar, multiplicar y dividir fracciones, este viaje guiado cubre todos los aspectos esenciales. Prepárate para sumergirte en un mundo de números y líneas, donde cada paso te acerca a dominar el arte de las fracciones.
Fracciones propias y fracciones impropias
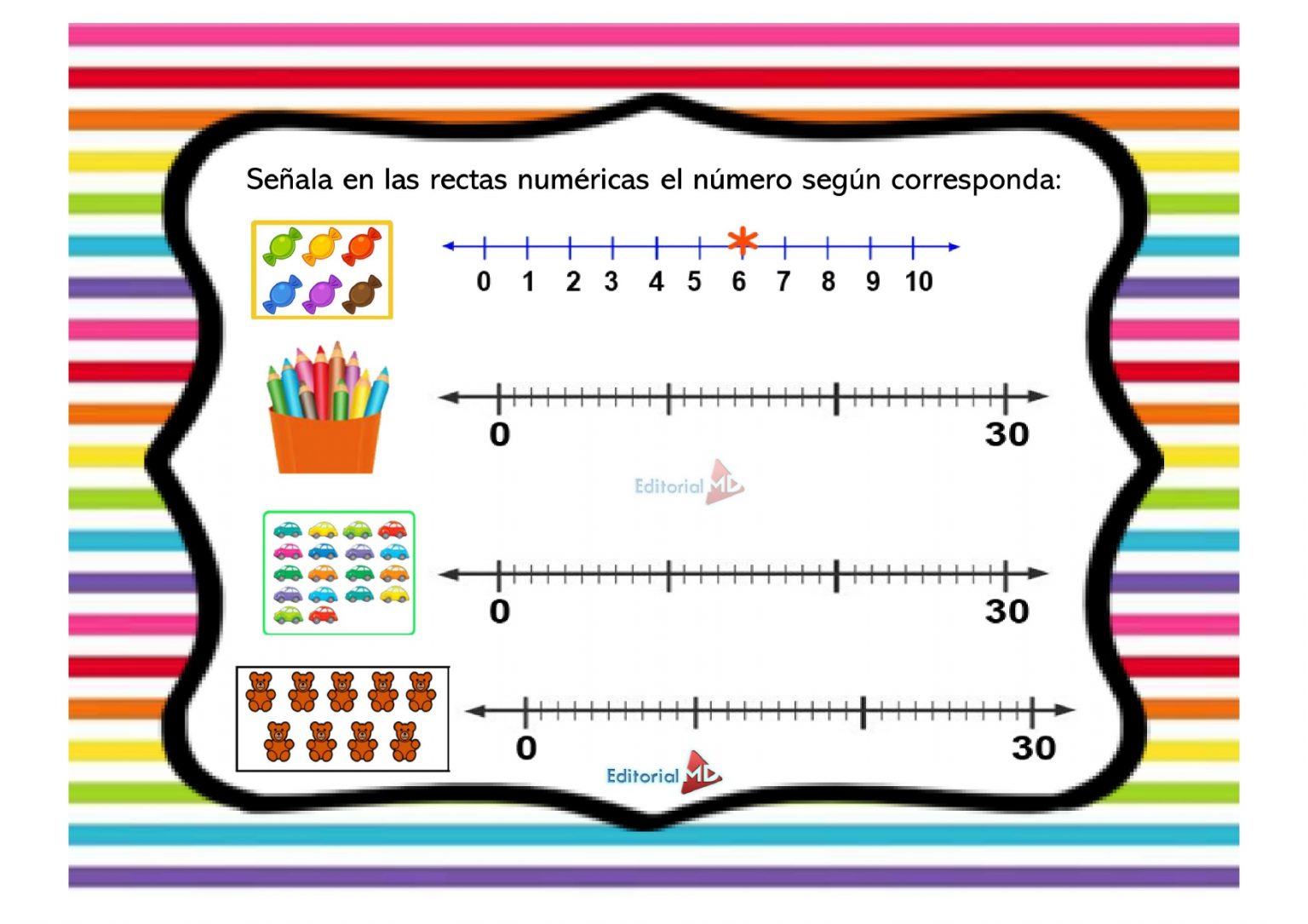
Las fracciones son números que representan partes de un todo. Las fracciones propias son aquellas en las que el numerador (el número superior) es menor que el denominador (el número inferior). Esto significa que la fracción representa una parte del todo que es menor que el todo.
Por ejemplo, la fracción 1/2 representa la mitad de un todo.Las fracciones impropias son aquellas en las que el numerador es mayor o igual que el denominador. Esto significa que la fracción representa una parte del todo que es mayor o igual que el todo.
Por ejemplo, la fracción 3/2 representa una parte del todo que es mayor que el todo.Para convertir una fracción impropia en un número mixto, dividimos el numerador por el denominador y escribimos el resto como fracción. Por ejemplo, para convertir la fracción impropia 5/2 en un número mixto, dividimos 5 entre 2 y obtenemos 2 con un resto de 1. Por lo tanto, el número mixto es 2 1/2.
Comparar y ordenar fracciones
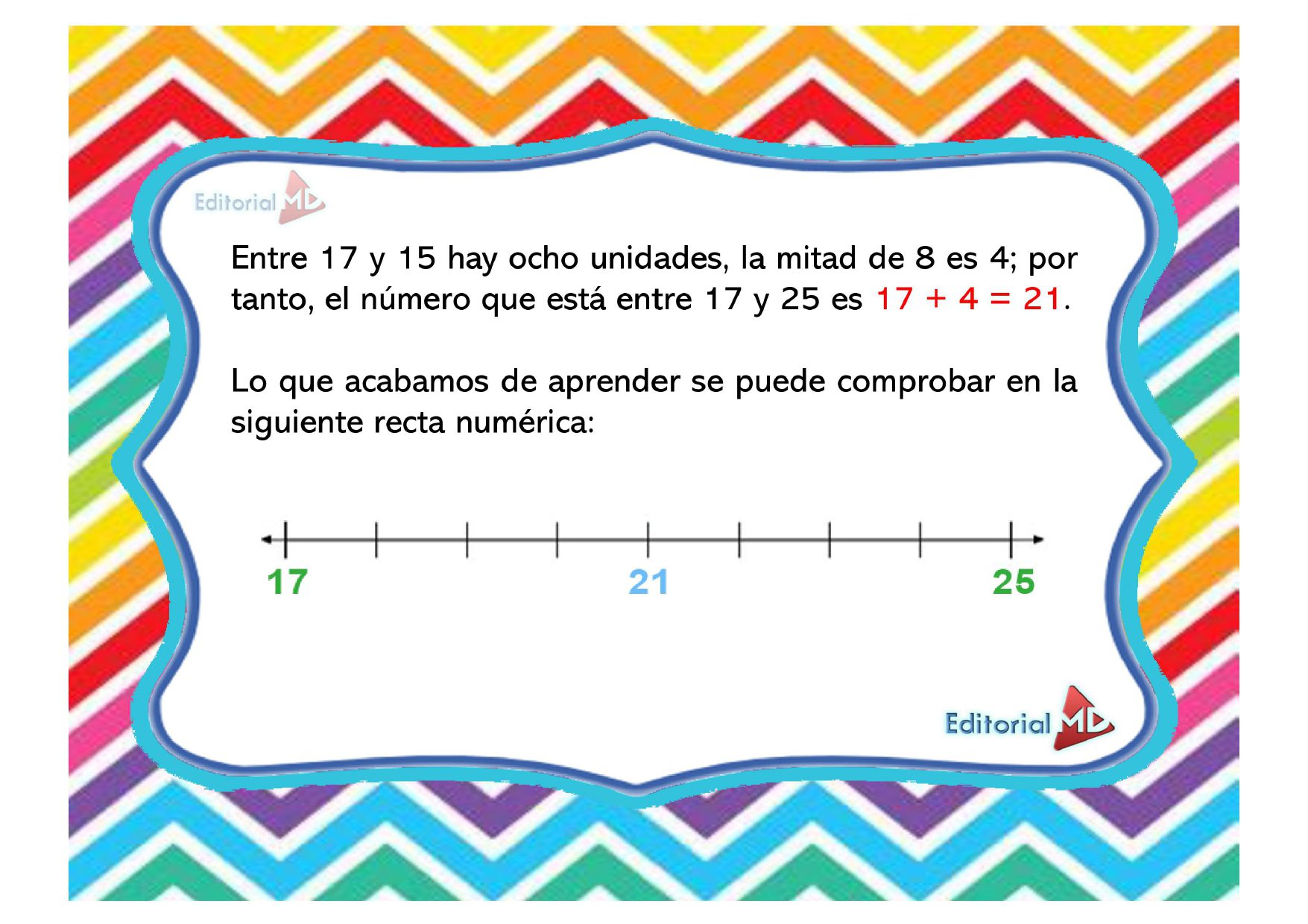
¡Hola chicos y chicas! Hoy vamos a aprender a comparar y ordenar fracciones. Es muy fácil, solo tenemos que seguir unos sencillos pasos.
Comparar fracciones con el mismo denominador
Si las fracciones tienen el mismo denominador, podemos compararlas directamente. La fracción con el numerador más grande es mayor. Por ejemplo:* 1/3 es menor que 2/3 porque 1 es menor que 2.
3/5 es mayor que 2/5 porque 3 es mayor que 2.
Comparar fracciones con diferentes denominadores
Cuando las fracciones tienen diferentes denominadores, necesitamos convertirlas a fracciones equivalentes con el mismo denominador. Para ello, multiplicamos el numerador y el denominador de cada fracción por el denominador de la otra fracción. Por ejemplo:* Para comparar 1/3 y 1/4, multiplicamos 1/3 por 4/4 (el denominador de 1/4) y 1/4 por 3/3 (el denominador de 1/3). Esto nos da 4/12 y 3/12, respectivamente.
Como 4 es mayor que 3, 1/3 es mayor que 1/4.
Ordenar un conjunto de fracciones de menor a mayor
Para ordenar un conjunto de fracciones de menor a mayor, podemos compararlas de dos en dos. Primero, comparamos la primera fracción con la segunda, luego la segunda con la tercera, y así sucesivamente. La fracción más pequeña siempre va primero.
Por ejemplo:* Para ordenar 1/2, 1/4 y 1/3 de menor a mayor, comparamos primero 1/2 y 1/
- Como 1/2 es mayor, lo colocamos primero. Luego, comparamos 1/2 y 1/
- Como 1/2 es menor, lo colocamos segundo. Finalmente, colocamos 1/3 en último lugar. Por lo tanto, el orden de las fracciones de menor a mayor es: 1/4, 1/2, 1/3.
¡Y eso es todo! Ahora ya sabes cómo comparar y ordenar fracciones. ¡Es muy fácil!
Sumar y restar fracciones: Fracciones En La Recta Numerica Para Niños De Primaria
Sumar y restar fracciones es una habilidad esencial en matemáticas. En esta sección, exploraremos cómo sumar y restar fracciones con el mismo denominador y diferentes denominadores.
Sumar y restar fracciones con el mismo denominador
Cuando las fracciones tienen el mismo denominador, podemos sumar o restar los numeradores y mantener el mismo denominador.
Ejemplo: Sumar 1/4 y 2/4
- Sumamos los numeradores: 1 + 2 = 3
- Mantenemos el mismo denominador: 4
- La suma es 3/4
Sumar y restar fracciones con diferentes denominadores
Cuando las fracciones tienen diferentes denominadores, primero debemos encontrar un denominador común.
El denominador común más pequeño (DCM) es el menor denominador común a ambas fracciones.
Ejemplo: Sumar 1/2 y 1/3
- El DCM de 2 y 3 es 6
- Convertimos las fracciones al DCM:
- 1/2 = 3/6
- 1/3 = 2/6
- Ahora podemos sumar los numeradores: 3 + 2 = 5
- Mantenemos el DCM como denominador: 6
- La suma es 5/6
Restar fracciones con diferentes denominadores
Para restar fracciones con diferentes denominadores, seguimos el mismo proceso que para sumar.
Ejemplo: Restar 1/2 de 1
- El DCM de 2 y 1 es 2
- Convertimos las fracciones al DCM:
- 1 = 2/2
- Ahora podemos restar los numeradores: 2
1 = 1
- Mantenemos el DCM como denominador: 2
- La resta es 1/2
Multiplicar y dividir fracciones

Multiplicar y dividir fracciones es una habilidad esencial en matemáticas. Aprenderemos cómo multiplicar y dividir fracciones, así como a simplificarlas después de realizar estas operaciones.
Multiplicar fracciones
Para multiplicar fracciones, simplemente multiplica los numeradores y los denominadores. Por ejemplo:
- 2/3 x 4/5 = (2 x 4) / (3 x 5) = 8/15
Dividir fracciones
Para dividir fracciones, invierte la segunda fracción (el divisor) y luego multiplica. Por ejemplo:
- 2/3 ÷ 4/5 = 2/3 x 5/4 = 10/12 = 5/6
Simplificar fracciones después de multiplicar o dividir, Fracciones En La Recta Numerica Para Niños De Primaria
Después de multiplicar o dividir fracciones, es importante simplificarlas si es posible. Para simplificar una fracción, divide el numerador y el denominador por su máximo común divisor (MCD).
- Por ejemplo, para simplificar 10/12, encontramos el MCD de 10 y 12, que es 2. Dividimos el numerador y el denominador por 2 para obtener 5/6.
Fracciones en la vida real

Las fracciones no son sólo conceptos matemáticos abstractos, sino que también son herramientas esenciales que utilizamos en nuestra vida cotidiana. Desde la cocina hasta la medición y la resolución de problemas, las fracciones nos ayudan a comprender y navegar el mundo que nos rodea.
En este módulo, exploraremos cómo las fracciones se utilizan en situaciones de la vida real. A través de ejemplos y actividades prácticas, descubriremos el poder y la versatilidad de las fracciones en nuestra vida diaria.
En la cocina
Las fracciones son indispensables en la cocina, donde se utilizan para medir ingredientes con precisión. Por ejemplo, una receta puede requerir 1/2 taza de azúcar o 3/4 de taza de harina. Estas fracciones nos permiten medir cantidades exactas de ingredientes, asegurando que nuestros platos salgan deliciosos y consistentes.
En la medición
Las fracciones también son cruciales en la medición. Cuando medimos distancias, por ejemplo, podemos utilizar fracciones para representar partes de una unidad. Una pulgada puede dividirse en 1/2 pulgada, 1/4 de pulgada o incluso 1/16 de pulgada. Estas fracciones nos permiten medir con precisión y comparar diferentes longitudes.
En la resolución de problemas
Las fracciones también juegan un papel importante en la resolución de problemas. Por ejemplo, podemos utilizar fracciones para representar partes de un todo o para comparar cantidades. Un problema puede pedirnos que encontremos la fracción de un número o que comparemos dos fracciones para determinar cuál es mayor.
Estas habilidades son esenciales para resolver problemas en una amplia gama de situaciones de la vida real.
A medida que concluimos nuestra exploración de las fracciones en la recta numérica, es evidente que estos conceptos aparentemente complejos se han transformado en herramientas poderosas para resolver problemas y comprender el mundo que nos rodea. Los estudiantes que han emprendido este viaje han adquirido no solo habilidades matemáticas, sino también una apreciación por la precisión y la lógica.
Que esta guía sirva como un trampolín para que los jóvenes exploradores continúen su aventura matemática, descubriendo nuevas alturas de comprensión y aplicando sus conocimientos a situaciones de la vida real. ¡El mundo de las fracciones los espera, lleno de posibilidades y listo para ser conquistado!
General Inquiries
¿Qué es una fracción propia?
Una fracción propia es aquella cuyo numerador es menor que su denominador, lo que significa que representa una parte menor que un todo.
¿Cómo se convierte una fracción impropia en un número mixto?
Para convertir una fracción impropia en un número mixto, divide el numerador entre el denominador. El cociente es la parte entera del número mixto, y el resto es el numerador de la fracción restante.
¿Cómo se comparan fracciones con diferentes denominadores?
Para comparar fracciones con diferentes denominadores, encuentra un denominador común. Multiplica el numerador y el denominador de cada fracción por un número que haga que los denominadores sean iguales.
